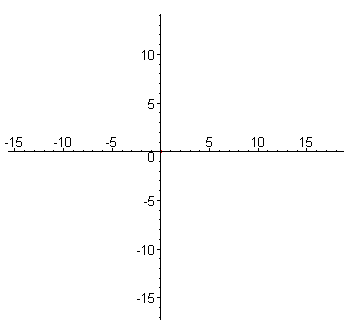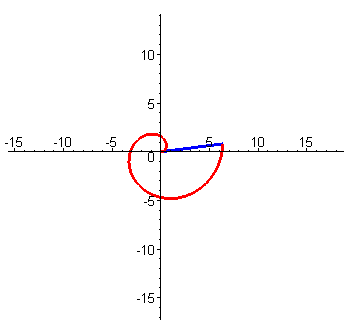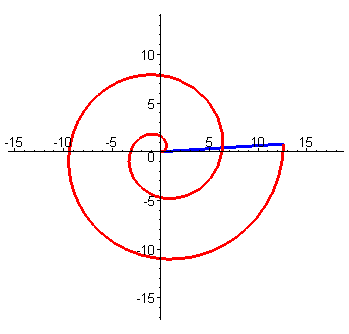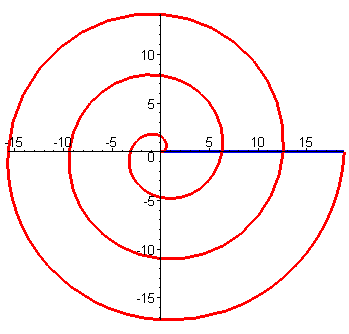函数
实数与函数
|
张瑞
中国科学技术大学数学科学学院
rui [at] ustc [dot] edu [dot] cn |
函数
定义 1.
设为非空数集,若有某种确定的关系(或对应关系),对于每个,都有唯一的一个实数与其对应,则称这个对应关系定义了从到中的函数,记为,或。
称为自变量,称为因变量,称为函数在处的值。
自变量的变化范围称为函数的定义域,记为。
当在定义域中任意变动时,函数值的变化范围称为函数的值域,记为。
若集合,则称为集合在函数下的像。
称为集合关于函数的原像。
函数的运算
-
-
-
-
称为和的复合函数
定义 2.
设。若存在函数,满足
和
则称是的反函数,记为,简记为。
- 反函数是唯一的。
- 反函数存在的充要条件是函数是一一的。
函数的表示方法
- 显式,
- 隐式,
- 参数式,
- 极坐标,
常见函数
- 常值函数:
- 取整函数:
- Dirichlet函数:
- Riemann函数:
基本初等函数
指数函数: ,
对数函数: ,
幂函数: ,
三角函数与反三角函数
从左图可以得到。类似有
|
,, , , 则 , |
得到
令, ,得到
得到
令, ,得到
公式
中,记, ,得到
因此,有
阿基米德螺线(Archimedean spiral)
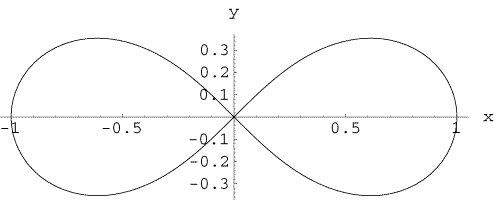
伯努利双纽线 (Lemniscate of Bernoulli)
平面上到两个定点距离的乘积等于两个定点距离一半的平方的点的轨迹,是伯努利双纽线。
解. 设定点为和,则两个定点距离一半为。点在双纽线上,则满足
两边平方,得到
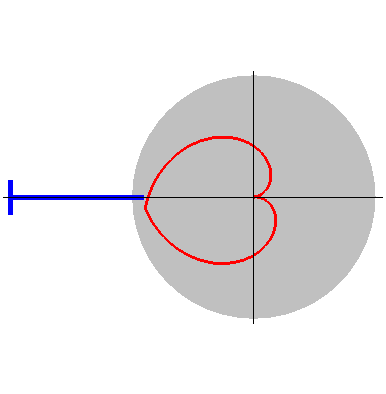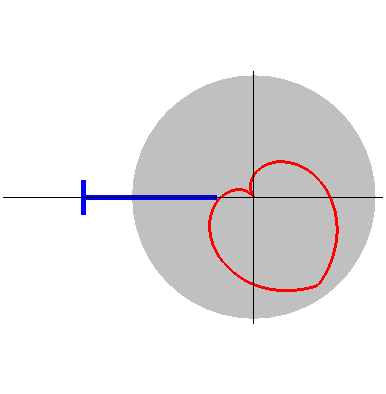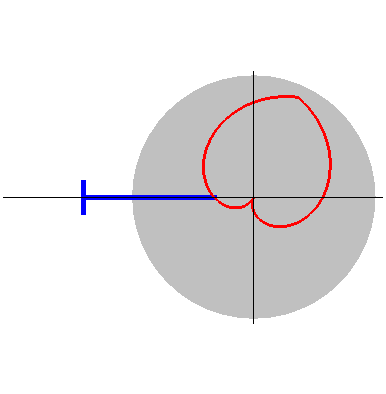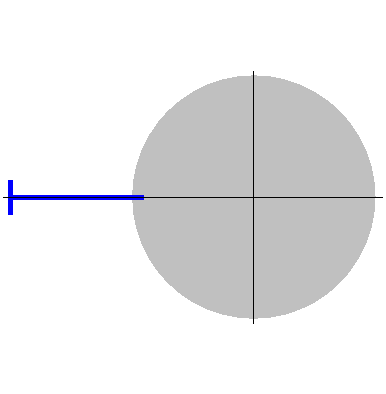
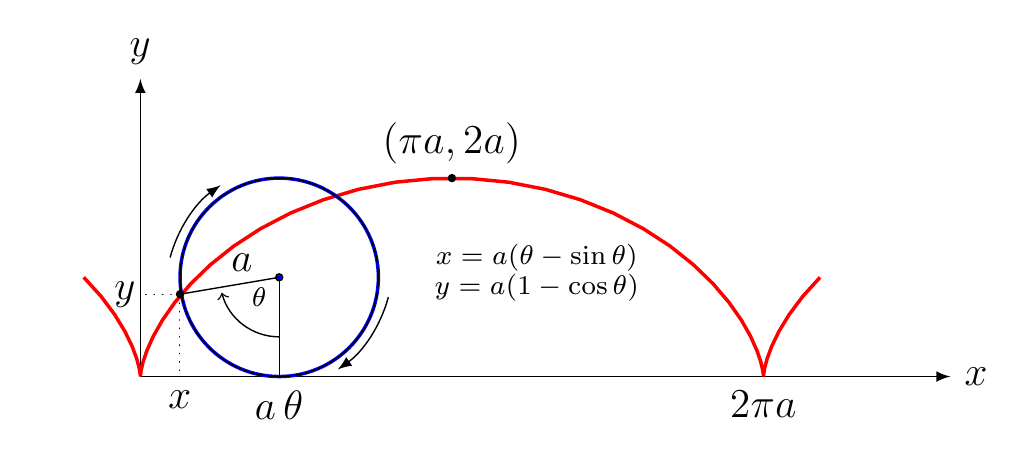
摆线 (cycloid)
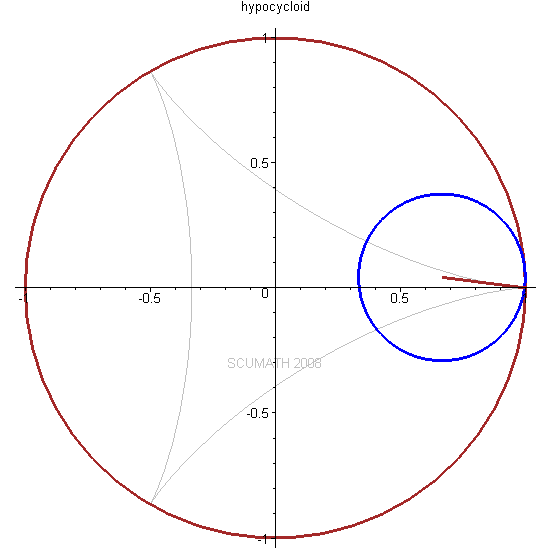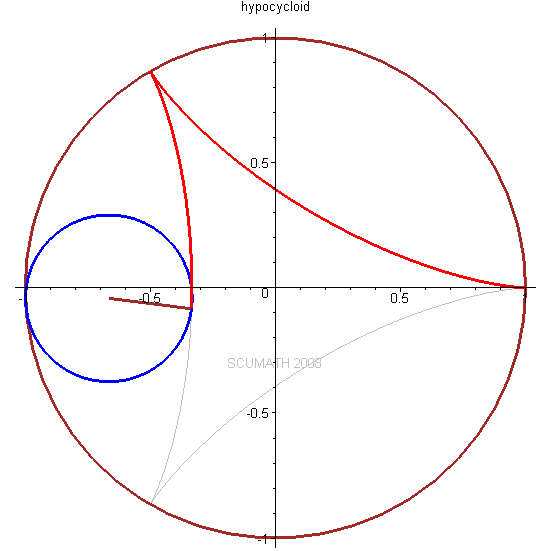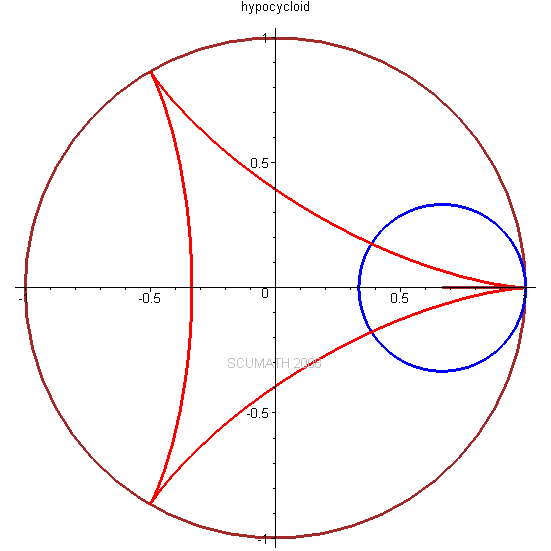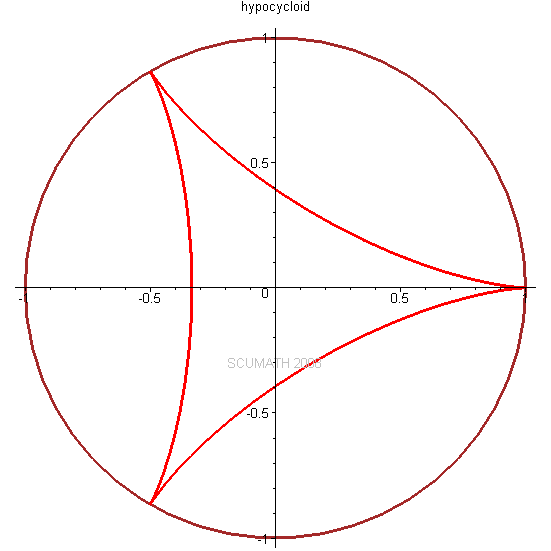
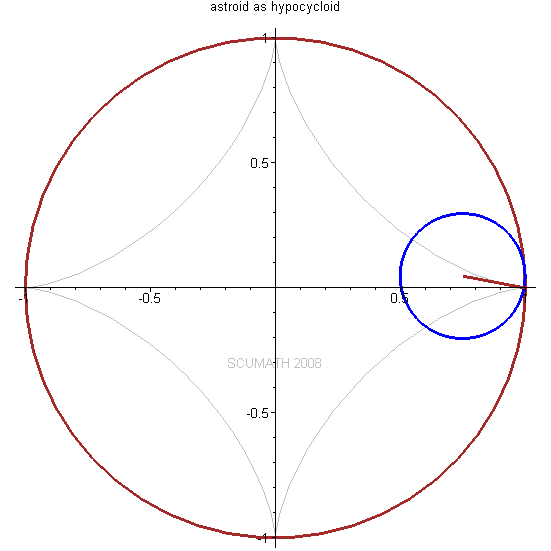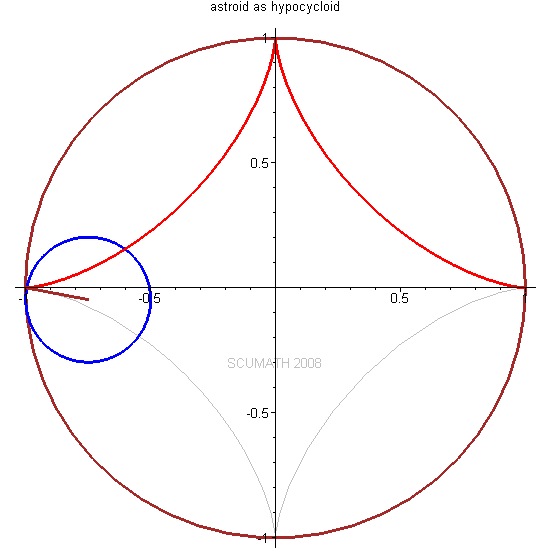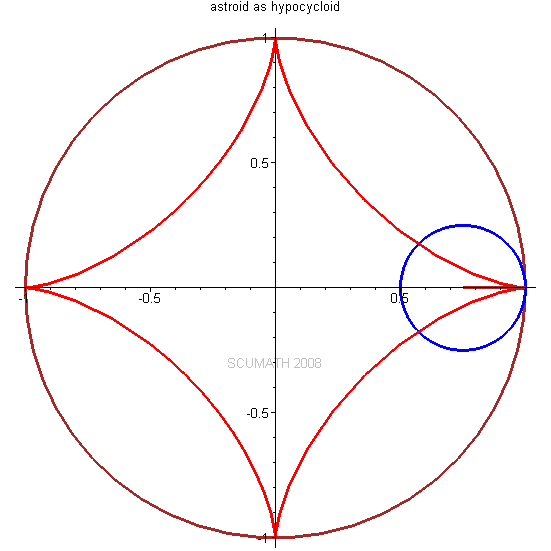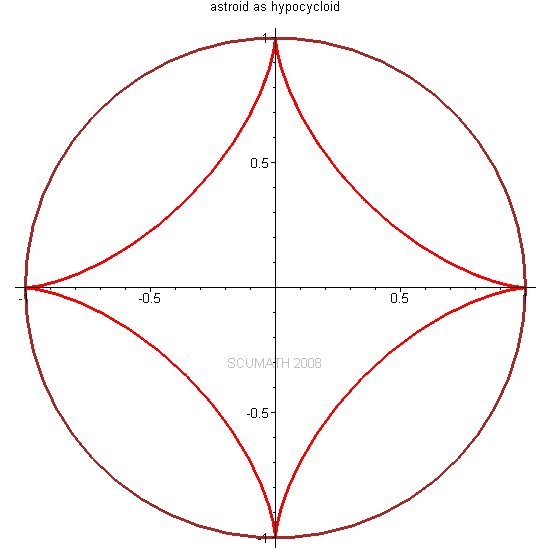
圆内摆线 (Hypocycloid)
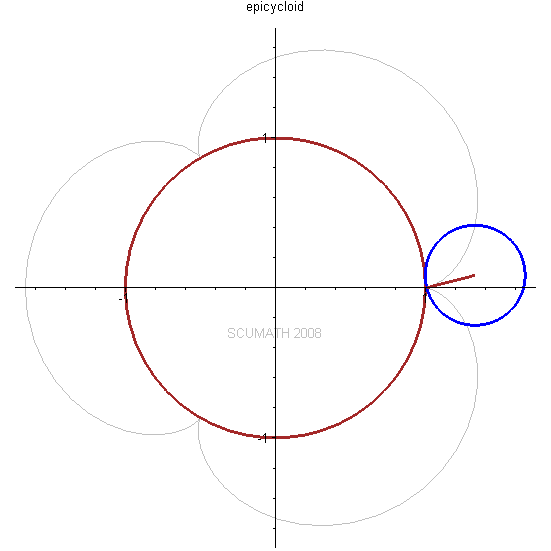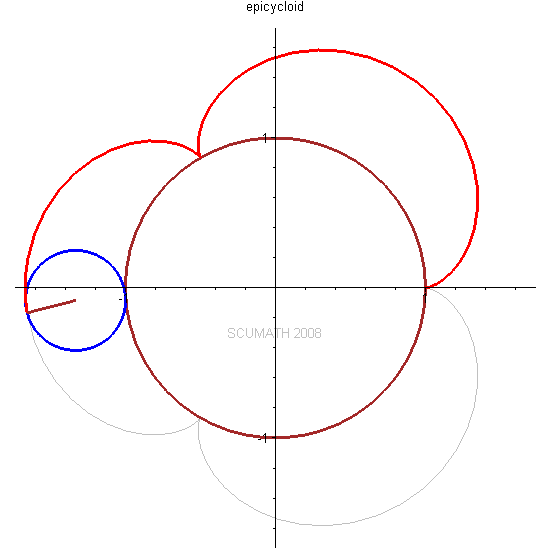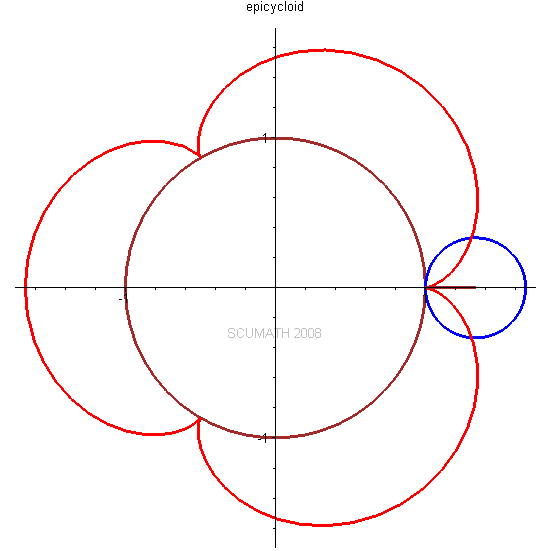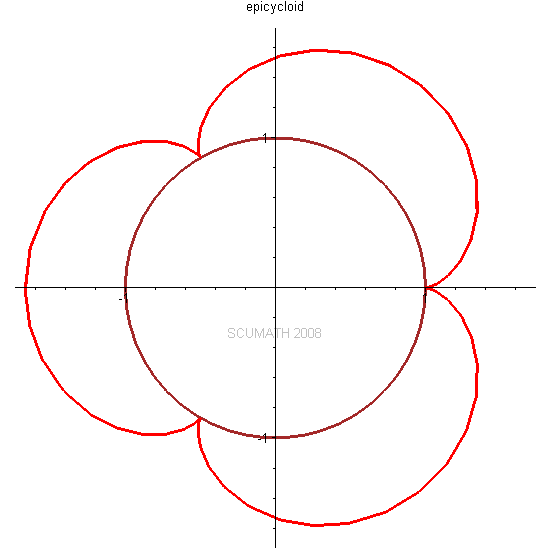
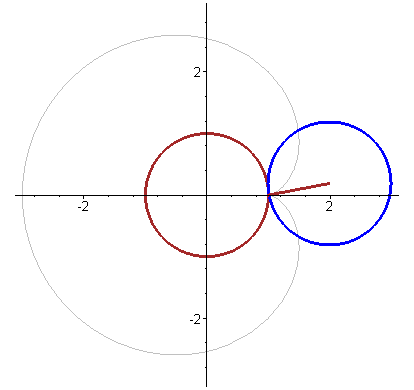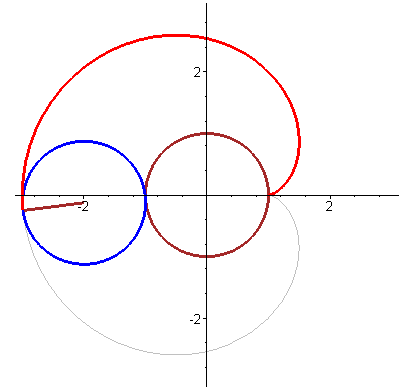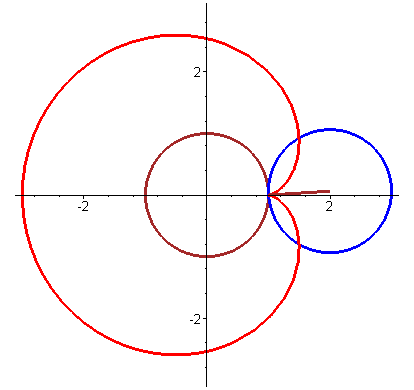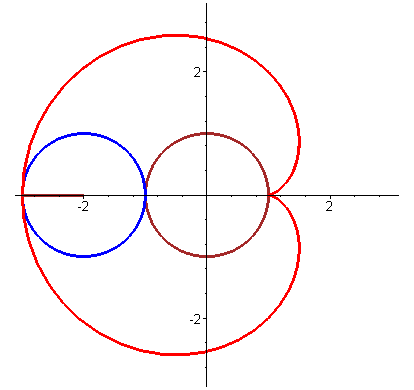
圆外摆线 (epicycloid)
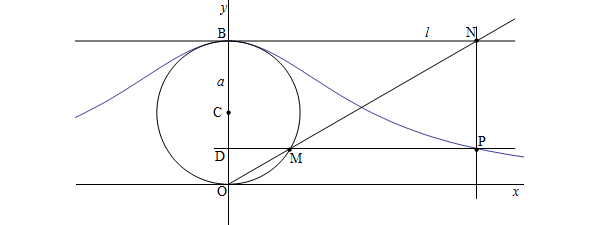
箕舌线 (The Witch of Agnesi)
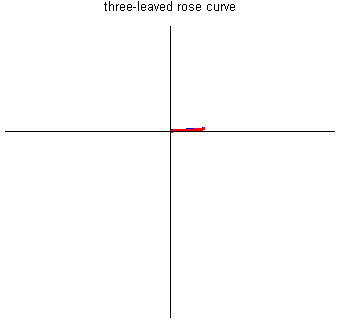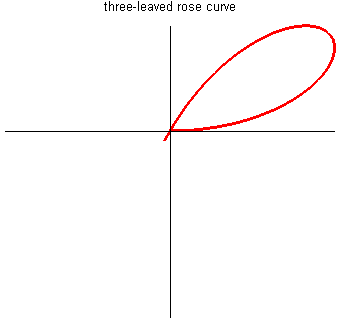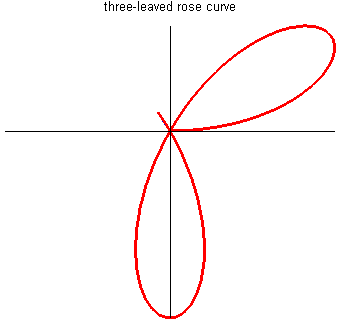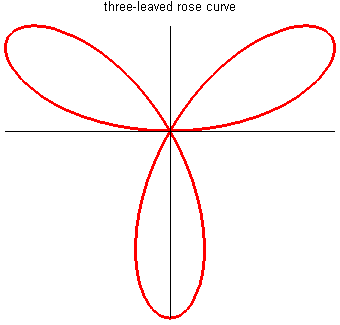
玫瑰线 (Rose Curve)
参数曲线
可以得到,是一个圆。
下图中
双曲线。 下图中
牛顿蛇形线。 下图中
牛顿三次曲线。 下图中
箕舌线 (The Witch of Agnesi)